展開とは
はじめに
皆さんこんにちは!筆者のゆちごんです!
今回は、高校数学最初の鬼門である、展開について学習していきます。
中学でも扱う内容ではありますが、高校数学での発展的な内容になるので、一緒に頑張りましょう!
文字式の乗法と分配法則
まず、本題に入る前に2つの要点を押さえておきます。
1つ目が文字式同士の乗法です。
これは実際の計算式を見ていただければ理解しやすいです。
・\(3a^2 \times 4a^4=12a^6\)
・\(x^3 \times x^2 \times y^5 \times y^2=x^5y^7\)
・\((3x^2y^4)^3=27x^6y^{12}\)
わかりやすく計算過程をまとめると以下のようになります。
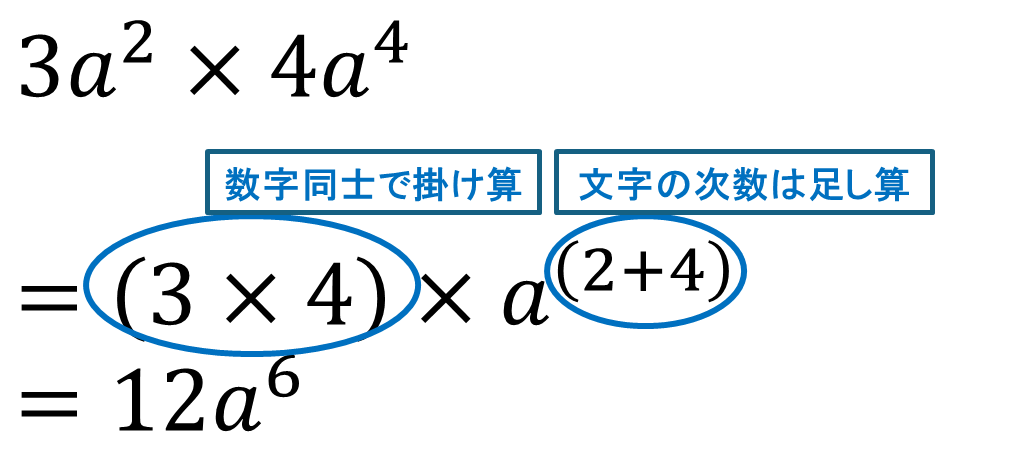
文字の次数の足し算は同じ文字同士で起こります!
次数について下の記事で詳しく解説しているので併せてどうぞ!
2つ目が分配法則です。
分配法則とは、(整式)×(整式)の計算をする時に用いる法則です。
以下に、分配法則の基本の計算を示します。

分配法則はその名の通り、()内に整式を掛けるときに、
()内の項全てに掛け算をおこなうことです。
まさに分配ってことですね!
展開の基本(中学までの復習)
さて!今回の本題である展開についてお話していきます。
まず、展開とは「単項式や多項式の積で表された式を計算して和の形に戻すこと」です。
つまり、上の分配法則の説明も「展開」に当たる訳ですね。
ここで(多項式)×(多項式)の展開を見ておきましょう。
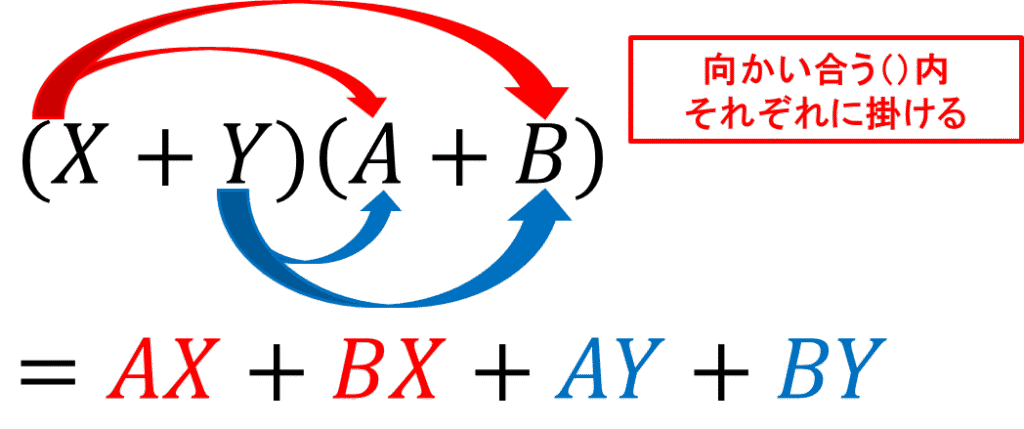
まず、これが展開の基本なので理解してください。
しかし、毎度全部掛けていたらめんどくさいですよね。
そんな時のために、規則性を持った式の場合の公式があります!
① \((a+b)^2=a^2+2ab+b^2\)
② \((a-b)^2=a^2-2ab+b^2\)
③ \((x+a)(x+b)=x^2+(a+b)x+ab\)
④ (\(x\)\(+\)\(a\))(\(x\)\(-\)\(a\))\(=x^2-a^2\)
多くて覚えれない…と思ったそこのあなた!安心してください。
①と③だけ理解しておけば大丈夫です。
まず、②は①の\(+b\)を\(-a\)に変えれば成り立つことがわかります。
①の規則性だけ抑えておくイメージですね。
次に、④も同様に③の\(+b\)を\(-a\)に変えて規則に適応すれば良いわけですね!
つまり、、、
④ (\(x\)+\(a\))(\(x-a\))
\(=x^2+\)(\(a\)\(-a\))\(x\)+{\((a) \times (-a)\)}
\(=x^2+0-a^2\)
\(=x^2-a^2\)
こんな感じです!
最後に例題を見てみましょう。
例題1
\((x+3)^2\)
\(=x^2+(2 \times x \times 3)+3^2\)
\(=x^2+6x+9\)
例題2
\((x-5)^2\)
\(=x^2-(2 \times x \times 5)+5^2\)
\(=x^2-10x+25\)
例題3
\((x+3)(x+4)\)
\(=x^2+(3+4)x+3 \times 4\)
\(=x^2+7x+12\)
例題4
\((x+2)(x-2)\)
\(=x^2+(2-2)x+2 \times (-2)\)
\(=x^2-4\)
がんばって展開の基本を身につけましょう!
展開(置き換えの利用)
いきなりですが、次の問題をご覧ください。
問題:次の式を展開せよ
\((x+y+3\))\((x+y-4)\)
上の問題は3×3の展開問題です。
これを今までの知識で解こうとすると、
\((x+y+3\))\((x+y-4)\)
=\(x^2+xy-4x+xy-4y+3x+3y-12\)
=\(x^2-x+2xy-y-12\)
少し長くなってしまって面倒くさいですよね・・・
ですからここで”工夫”してみます!
式をよく見ると、\(x+y\)の部分が共通していますよね。そこを利用します!
下の式をご覧ください!
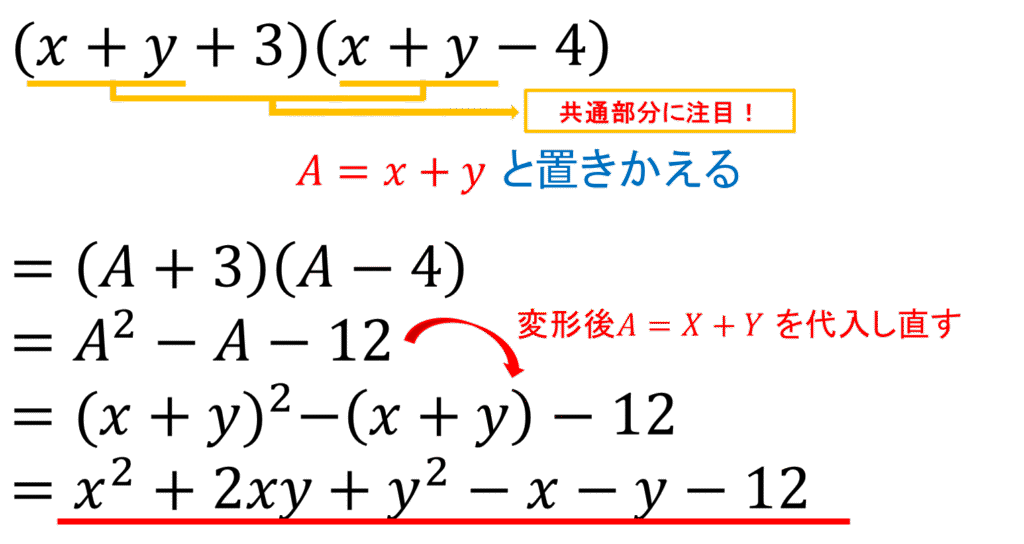
共通部分を見つけ、置き換えることで公式を適用できる形にするんですね!
これだけだと有用性を感じづらいかもしれませんが、もっと複雑な場面で力を発揮します!
がんばって理解しましょう!
展開(順序の工夫)
さて、この章もいきなりですが問題です。
問題:次の式を展開せよ
\((x+1)(x+2)(x+3)(x+4)\)
今までと違い掛けるべき多項式が4つもあります。
これを無理やり展開してみると...
\((x+1)(x+2)(x+3)(x+4)\)
=(\(x^2+3x+2\))(\(x+3\))(\(x+4\))
=(\(x^3+3x^2+2x+3x^2+9x+6\))(\(x+4\))
=(\(x^4+3x^3+2x^2+3x^3+9x^2+6x+4x^3+12x^2+8x+12x^2+36x+24\))
=(\(x^4+10x^35x^2+50x+24\))
となります!
なかなか大変な作業になってしまいますね。
確かに解けないこともないですが、計算ミスをしてしまったり、試験では時間制限があるので
時間内に間に合わなくなってしまいます!
また、多項式が5つ、6つと増えるともっと厳しくなるのは明白ですね!
そこで、「掛け算は順序を入れ替えて計算しても答えが同じ」という性質を用いて計算していきます!
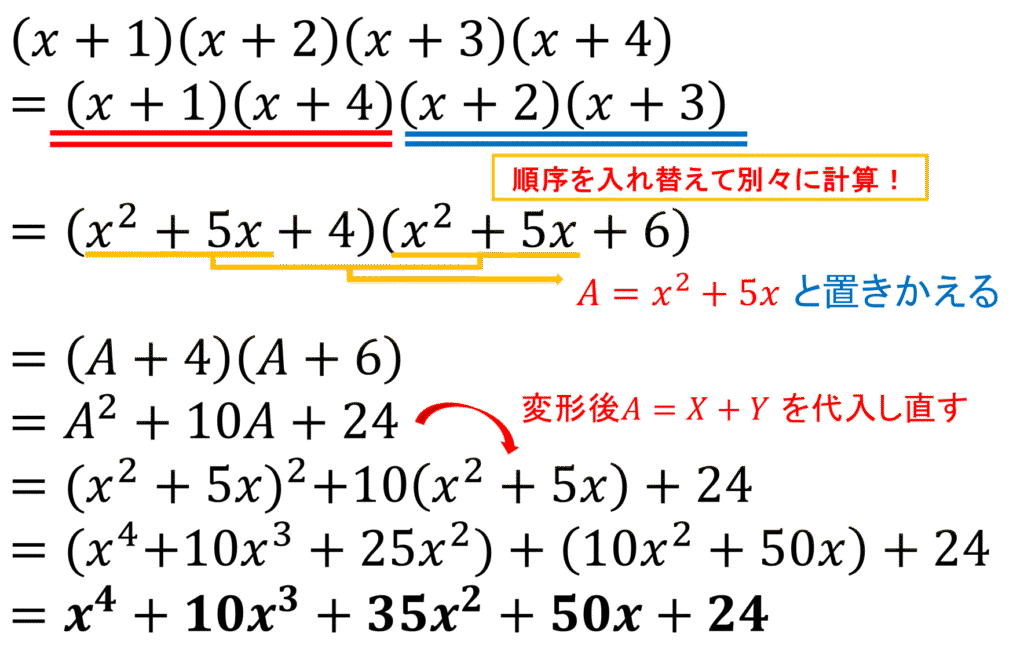
こんな感じです!
常に公式を使える形を探すようにすると、計算ミスも起きずらくなります。
それで共通部分が出てきたら、前節で学習した”置き換え”の知識を使うんですね!
高校で習う展開公式
高校で覚えてほしい公式がいくつかあります。
複雑な形をしているように見えますが簡単です!
マストで覚えるべきは5つです!がんばって覚えましょう。
1. \((a+b+c)^2\)=\(a^2+b^2+c^2+2ab+2bc+2ca\)
2. \((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
3. \((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
今までの公式と比較して覚えずらいですよね...
でも大丈夫!次の1点だけ抑えれば簡単に覚えられます!それは、
「2乗には2乗、3乗には3乗の項しか出てこない」
ということです!
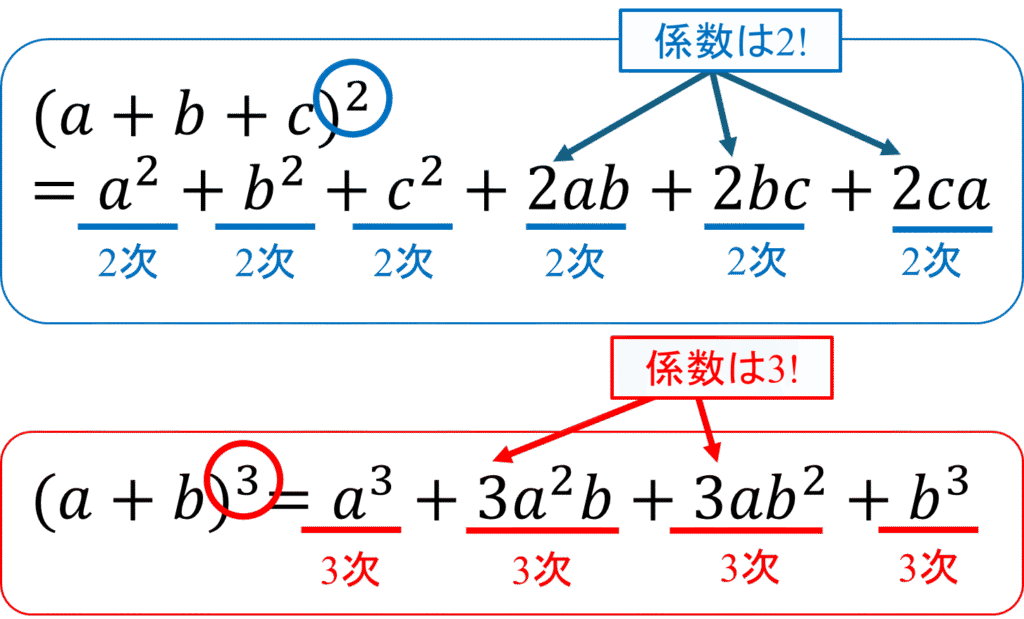
上図のようにすると簡単に覚えられます。
同じ次数しか出ないことに加えて、文字をa, b, cと変えていくだけです。
さらに、係数も2乗の展開式だと2で,3乗の展開式だと3になります。
3. \((a-b)^3\)の公式は4. \((a+b)^3\)の展開式でbが奇数個になる項を \(-\)にするだけです!
次にまとめて覚える公式は下の2つです。
4. \((a+b)(a^2-ab+b^2)=a^3+b^3\)
5. \((a-b)(a^2+ab+b^2)=a^3-b^3\)
正直、この2つは一度自分で展開してみると感覚的に理解して覚えることが出来ると思います。
4. \((a+b)(a^2-ab+b^2)\)
=\(a^3-a^2b+ab^2+a^2b-ab^2+b^3\)
=\(a^3+b^3\)
5. \((a-b)(a^2+ab+b^2)\)
=\(a^3+a^2b+ab^2-a^2b-ab^2-b^3\)
=\(a^3-b^3\)
真ん中の項が消えて、\(a^3\)と\(b^3\)が出てくるだけなので頭の中で組み立てましょう!
最後に
ここまで長かったですがお疲れさまでした!
まだまだ複雑な展開はありますが、ここに記していることを理解してもらえれば
後は応用していくだけです。
どんどん演習していきましょう。
解説してほしいものがあれば、随時お応えするのでリクエストお待ちしています!



コメント