数と式①　～整式と基本用語～　

整式について

はじめに

皆さんこんにちは！筆者のゆちごんです！
今回は高校数学の１番最初の単元である、整式について学習していきます。
中学数学の内容と被ることも多いですが、高校独自のものもあるためつまづかない様に一緒に頑張りましょう！

単項式と多項式とは

まずはこれから数学を学習していく上で、基本的な用語を抑えていきます。

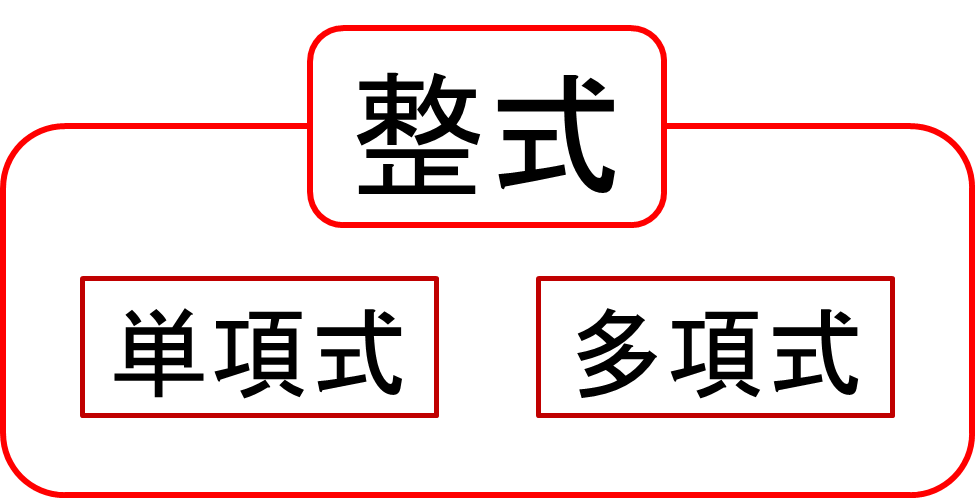
1. 整式　　→　単項式＋多項式　のこと
2. 単項式　→　数、文字（変数）、またそれらの積で表される式のこと
3. 多項式　→　単項式の和で表された式のこと

んーーーー？って感じですよね。
次を見ていただけたら理解できると思います。

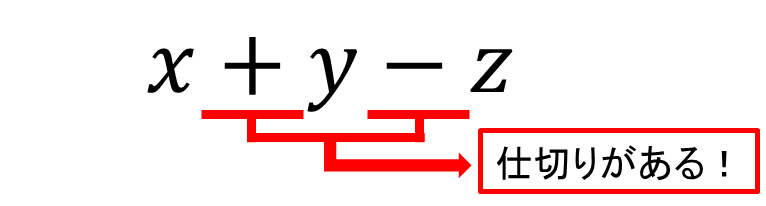
多項式　→　\(2x+4，x-3y，a^2+b，x+y-z\) and more…
これら全て多項式です！つまり多項式とは単項式を足し算、引き算で繋げたもののことです。

要するに言葉通り、“単” か “多” かってだけですね！

係数とは

続いて係数について学習します。
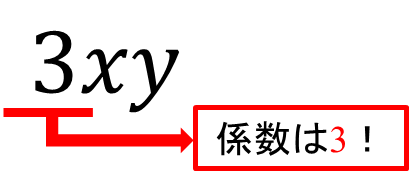
係数とは、「単項式に着目した時の数字の部分」です。
例えば、\(3xy\)の係数は\(3\)になります。

ただ、単純に係数は数字の部分というわけではありません。
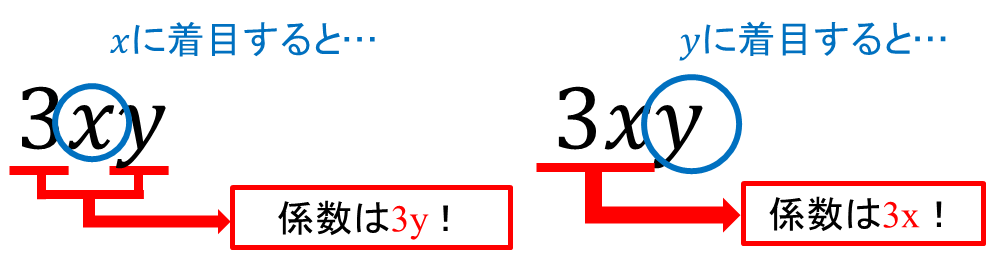
どの文字に着目するかで、係数は変化します。
上の\(3xy\)で考えると、\(x\)に着目すると係数は\(3y\)，\(y\)に着目すると係数は\(3x\)です。

場合によっては係数は文字も含むことがあると覚えておきましょう。

項とは

次に、散々出てきた項について学習します。
単“項”式、多“項”式の部分ですね！
簡単に言うと項とは「整式に着目した時の＋で区切られた部分」です。
例えば、\(2x+5y-7z^2\)の項は\(2x\)，\(5y\)，\(-7z^2\)です。

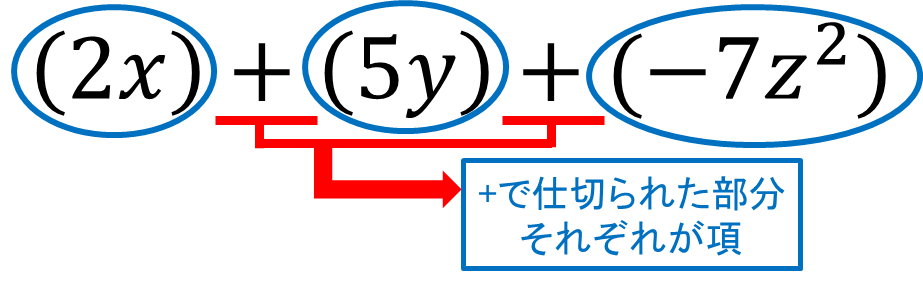
あくまで＋で区切られた部分なので－の扱いに注意しましょう。

N次式（何次式）、次数とは

まず、次数について学習します。
次数とは「掛け合わされている文字の個数」のことです。
・\(3x\)の次数は\(1\)
・\(x^2\)の次数は\(2\)
・\(2xyz\)の次数は\(3\)

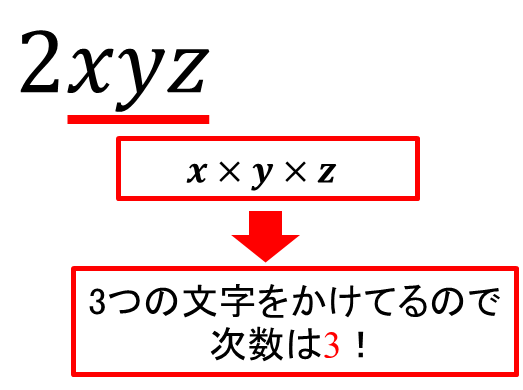
ただ、次数もどの文字に着目するかで変化します。

着目した文字以外は、数字と同じように扱うということですね！

これらを踏まえて次の問題を考えてみましょう。

問題：\(2x^3+x^2+3\)は何次式か答えよ。

何次式かの考え方は以下の通りです。

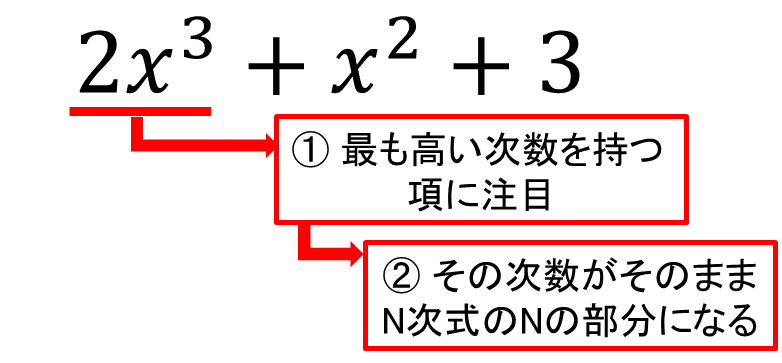
つまり、上記の場合は\(3\)次式になります。
また、これもどの文字に着目するかで答えが変わるので気を付けてください。
あえて言うなら、上は\(x\)に着目した場合です。

降べきの順と昇べきの順とは

最後に、「降べき」の順と「昇べき」の順について学習します。
まず、降べきの順とは「ある文字に着目して次数が高い順に並び変えること」です。
反対に、昇べきの順とは「ある文字に着目して次数が低い順に並び変えること」です。
次の問題を考えてみましょう。

問題：\(5x^2+x^4+6x^3-4x\)を降べきの順に並び替えよ。

以下のように考えます。

したがって答えは、\(x^4+6x^3+5x^2-4x\)です！

ちなみに昇べきの順について整理するときは、低い順、つまり反対に並び替えるので、

答えは、\(-4x+5x^2+6x^3+x^4\)です！
何度も言いますが、これは\(x\)に着目しているからこの並び替えができるわけです。

次に、\(x\)と\(y\)が混同している場合について考えましょう。

問題：\(x^3+4xy+x^4+3y^4-7x+3y\)を降べきの順に並び替えよ。

この問題は\(x\)について整理するか、\(y\)について整理するかで変わってきます。

（a）\(x\)について整理すると、
　　　\(x^3+4xy+x^4+3y^4-7x+3y\)
　　　\(=x^4+x^3+4xy-7x+3y^4+3y\)
　　　\(=x^4+x^3+(4y-7)x+3y^4+3y\)

（b）\(y\)について整理すると、
　　　\(x^3+4xy+x^4+3y^4-7x+3y\)
　　　\(=3y^4+3y+4xy+x^4+x^3-7x\)
　　　\(=3y^4+(3+4x)y+x^4+x^3-7x\)

と2通りの答えが出てきます！
問題として出てくるときには、どの文字について整理するか指定されています。
指定されていないときには、基本的に\(x\)について整理すると考えていただいて大丈夫です。

降べき、昇べきの順の考え方は、後に出てくる「因数分解」の章で役に立つので覚えておきましょう！

最後に

今回の単元では整式と基本的な用語について学習しました。
簡単と侮るなかれ。最初でつまづくと後々致命的な遅れとなるので、しっかりと復習しましょう。
お疲れさまでした！！